7.6 复数值特征值

在本节中，我们再次考虑具有常系数的 $n$ 个线性齐次方程组

$$\begin{equation*} \mathbf{x}^{\prime}=\mathbf{A x} \tag{1} \end{equation*}$$

其中系数矩阵 $\mathbf{A}$ 是实数值的。 如果我们寻求 $\mathbf{x}=\boldsymbol{\xi} e^{r t}$ 形式的解，那么与 7.5 节中一样， $r$ 必须是特征值，而 $\boldsymbol{\xi}$ 是系数矩阵 $\mathbf{A}$ 的相应特征向量。 回顾一下，$\mathbf{A}$ 的特征值 $r_{1}, \ldots, r_{n}$ 是特征方程的根

$$\begin{equation*} \operatorname{det}(\mathbf{A}-r \mathbf{I})=0 \tag{2} \end{equation*}$$

并且相应的特征向量是满足

$$\begin{equation*} (\mathbf{A}-r \mathbf{I}) \boldsymbol{\xi}=\mathbf{0} . \tag{3} \end{equation*}$$

如果 $\mathbf{A}$ 是实数值的，那么 $r$ 的多项式方程 (2) 中的系数是实数值的，并且任何复数值特征值必须以共轭对的形式出现。 例如，如果 $r_{1}=\lambda+i \mu$，其中 $\lambda$ 和 $\mu$ 是实数，是 $\mathbf{A}$ 的特征值，那么 $r_{2}=\lambda-i \mu$ 也是。 为了探讨复数值特征值的影响，我们从一个例子开始。

示例 1

求系统

$$\mathbf{x}^{\prime}=\left(\begin{array}{rr} -\frac{1}{2} & 1 \tag{4}\\ -1 & -\frac{1}{2} \end{array}\right) \mathbf{x}$$

的一组实数值基本解。 绘制一个相图和典型解的分量图。

解：

系统 (4) 的方向场如图 7.6.1 所示。 该图表明相平面中的轨迹顺时针螺旋向原点。

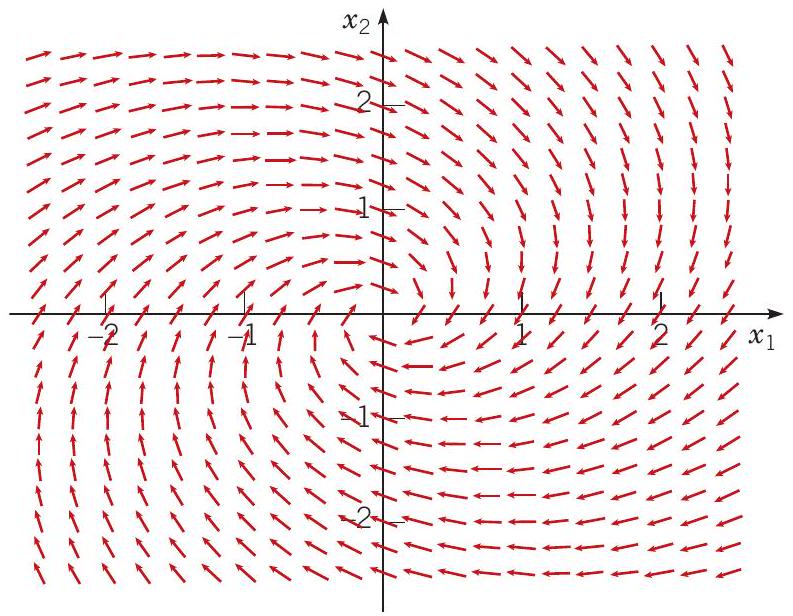
图 7.6.1 系统 (4) 的方向场。

为了找到一组基本解，我们假设

$$\begin{equation*} \mathbf{x}=\boldsymbol{\xi} e^{r t} \tag{5} \end{equation*}$$

并获得线性代数方程组

$$\left(\begin{array}{cc} -\frac{1}{2}-r & 1 \tag{6}\\ -1 & -\frac{1}{2}-r \end{array}\right)\binom{\xi_{1}}{\xi_{2}}=\binom{0}{0}$$

用于求 $\mathbf{A}$ 的特征值和特征向量。 特征方程为

$$\left|\begin{array}{cc} -\frac{1}{2}-r & 1 \tag{7}\\ -1 & -\frac{1}{2}-r \end{array}\right|=r^{2}+r+\frac{5}{4}=0$$

因此，特征值为 $r_{1}=-\frac{1}{2}+i$ 和 $r_{2}=-\frac{1}{2}-i$。 从方程 (6) 可以看出，一个简单的计算表明，相应的特征向量为

$$\begin{equation*} \boldsymbol{\xi}^{(1)}=\binom{1}{i}, \quad \boldsymbol{\xi}^{(2)}=\binom{1}{-i} . \tag{8} \end{equation*}$$

观察到特征向量 $\boldsymbol{\xi}^{(1)}$ 和 $\boldsymbol{\xi}^{(2)}$ 也是复共轭。 因此，系统 (4) 的一组基本解为

$$\begin{equation*} \mathbf{x}^{(1)}(t)=\binom{1}{i} e^{(-1 / 2+i) t}, \quad \mathbf{x}^{(2)}(t)=\binom{1}{-i} e^{(-1 / 2-i) t} \tag{9} \end{equation*}$$

为了获得一组实数值解，我们可以（根据定理 7.4.5）选择 $\mathbf{x}^{(1)}$ 或 $\mathbf{x}^{(2)}$ 的实部和虚部。 事实上，

$$\begin{equation*} \mathbf{x}^{(1)}(t)=\binom{1}{i} e^{-t / 2}(\cos t+i \sin t)=\binom{e^{-t / 2} \cos t}{-e^{-t / 2} \sin t}+i\binom{e^{-t / 2} \sin t}{e^{-t / 2} \cos t} \tag{10} \end{equation*}$$

因此，方程 (4) 的一对实数值解为

$$\begin{equation*} \mathbf{u}(t)=e^{-t / 2}\binom{\cos t}{-\sin t}, \quad \mathbf{v}(t)=e^{-t / 2}\binom{\sin t}{\cos t} \tag{11} \end{equation*}$$

为了验证 $\mathbf{u}(t)$ 和 $\mathbf{v}(t)$ 是线性无关的，我们计算它们的 Wronskian 行列式：

$$W[\mathbf{u}, \mathbf{v}](t)=\left|\begin{array}{cc} e^{-t / 2} \cos t & e^{-t / 2} \sin t \\ -e^{-t / 2} \sin t & e^{-t / 2} \cos t \end{array}\right|=e^{-t}\left(\cos ^{2} t+\sin ^{2} t\right)=e^{-t}$$

Wronskian 行列式 $W[\mathbf{u}, \mathbf{v}](t)$ 永远不为零，因此得出结论：$\mathbf{u}(t)$ 和 $\mathbf{v}(t)$ 构成系统 (4) 的一组（实数值）基本解。

解 $\mathbf{u}(t)$ 和 $\mathbf{v}(t)$ 的图分别显示为图 7.6.2(a) 中的实线和虚线黑色曲线，该图是系统 (4) 的相图。 由于

$$\mathbf{u}(0)=\binom{1}{0}, \quad \mathbf{v}(0)=\binom{0}{1}$$

“ $\mathbf{u}(t)$ 和 $\mathbf{v}(t)$ 的图像分别通过点 $(1,0)$ 和 $(0,1)$。系统 (4) 的其他解是 $\mathbf{u}(t)$ 和 $\mathbf{v}(t)$ 的线性组合，并且图 7.6.2(a) 中也显示了其中一些解的图像。当 $t \rightarrow \infty$ 时，每个轨迹都沿着螺旋路径接近原点，围绕原点进行无限多次旋转；这是由于解 (11) 是衰减指数和正弦或余弦因子的乘积。图 7.6.2(b) 显示了一些 $x_{1}$ 相对于 $t$ 的典型图像；每一个都代表着随时间衰减的振荡。图 7.6.2(c) 显示了相应的 $x_{2}$ 相对于 $t$ 的图像。

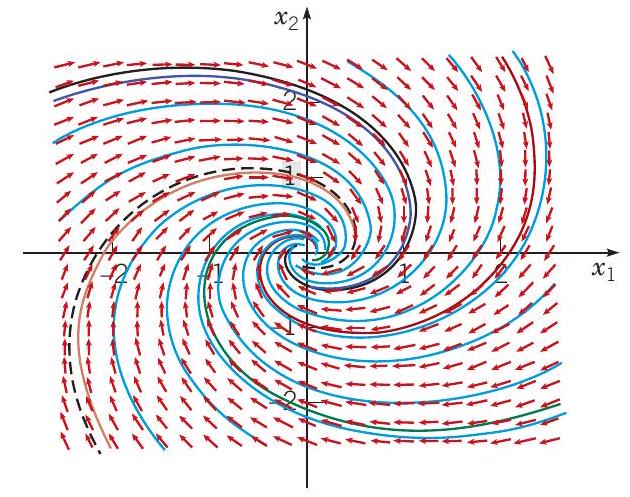
(a)

(b)

(c)

图 7.6.2 (a) 系统 (4) 的相图；原点是一个螺旋点。(b) 系统 (4) 的 $x_{1}$ 相对于 $t$ 的图。(c) 系统 (4) 的 $x_{2}$ 相对于 $t$ 的图。 (b) 和 (c) 中的分量图根据它们在 (a) 中的轨迹进行颜色编码。黑色实曲线表示通过 $(1,0)$ 的解 $\mathbf{u}(t)$，黑色虚曲线表示通过 $(0.1)$ 的 $\mathbf{v}(t)$，紫色曲线通过 $(1,1)$，红色通过 $(-1,1)$，绿色通过 $(-1,-1)$，橙色通过 $(1,-1)$。

图 7.6.2(a) 是所有 $2 \times 2$ 系统 $\mathbf{x}^{\prime}=\mathbf{A x}$ 的典型代表，这些系统的特征值是具有负实部的复数。原点被称为螺旋点，并且是渐近稳定的，因为所有轨迹都随着 $t$ 的增大而接近它。对于特征值具有正实部的系统，轨迹类似于图 7.6.2(a) 中的轨迹，但运动方向远离原点，并且轨迹变得无界。在这种情况下，原点是不稳定的。

如果特征值的实部为零，那么轨迹既不接近原点，也不会变得无界，而是重复地遍历原点周围的闭合曲线。这种行为的例子可以在下面的图 7.6.3(b) 和 7.6.4(b) 中看到。在这种情况下，原点被称为中心，并且据说是稳定的，但不是渐近稳定的。在这三种情况下，运动方向可以是顺时针，如本例所示，也可以是逆时针，具体取决于系数矩阵 $\mathbf{A}$ 的元素。

图 7.6.2(a) 中的相图是由计算机绘制的，但是可以手动生成相图的有用草图。我们已经注意到，当特征值 $\lambda \pm i \mu$ 是复数时，轨迹要么向内螺旋 ($\lambda<0$)，要么向外螺旋 ($\lambda>0$)，要么重复地遍历闭合曲线 ($\lambda=0$)。为了确定运动方向是顺时针还是逆时针，我们只需要确定一个方便点的运动方向。例如，在系统 (4) 中，我们可以选择 $\mathbf{x}=(0,1)^{T}$。那么 $\mathbf{A} \mathbf{x}=\left(1,-\frac{1}{2}\right)^{T}$。因此，在相平面中的点 $(0,1)$ 处，该点轨迹的切向量 $\mathbf{x}^{\prime}$ 具有正的 $x_{1}$ 分量，因此从第二象限指向第一象限。因此，该系统每个轨迹的运动方向都是顺时针方向。

回到线性微分方程的一般系统 (1)

$$\mathbf{x}^{\prime}=\mathbf{A} \mathbf{x}$$

我们可以像在例子中那样进行。假设有一对复共轭特征值，$r_{1}=\lambda+i \mu$ 和 $r_{2}=\lambda-i \mu$。那么相应的特征向量 $\boldsymbol{\xi}^{(1)}$ 和 $\boldsymbol{\xi}^{(2)}$ 也是复共轭的。要看到这一点，回想一下 $r_{1}$ 和 $\boldsymbol{\xi}^{(1)}$ 满足

$$\begin{equation*} \left(\mathbf{A}-r_{1} \mathbf{I}\right) \boldsymbol{\xi}^{(1)}=\mathbf{0} \tag{12} \end{equation*}$$

对该方程取复共轭，并注意到 $\mathbf{A}$ 和 $\mathbf{I}$ 是实数值的，我们得到

$$\begin{equation*} \overline{\left(A-r_{1} I\right) \boldsymbol{\xi}^{(1)}}=\left(\mathbf{A}-\overline{r_{1}} \mathbf{I}\right) \overline{\boldsymbol{\xi}^{(1)}}=\mathbf{0}, \tag{13} \end{equation*}$$

其中 $\overline{r_{1}}$ 和 $\overline{\boldsymbol{\xi}^{(1)}}$ 分别是 $r_{1}$ 和 $\boldsymbol{\xi}^{(1)}$ 的复共轭。换句话说，$r_{2}=\overline{r_{1}}$ 也是一个特征值，并且 $\boldsymbol{\xi}^{(2)}=\overline{\boldsymbol{\xi}^{(1)}}$ 是一个对应的特征向量。相应的解

$$\begin{equation*} \mathbf{x}^{(1)}(t)=\boldsymbol{\xi}^{(1)} e^{r_{1} t}, \quad \mathbf{x}^{(2)}(t)=\overline{\boldsymbol{\xi}^{(1)}} e^{\overline{r_{1}} t} \tag{14} \end{equation*}$$

微分方程(1)的解因此是彼此的复共轭。因此，如例1所示，我们可以通过取方程(14)给出的$\mathbf{x}^{(1)}(t)$或$\mathbf{x}^{(2)}(t)$的实部和虚部，找到对应于特征值$r_{1}$和$r_{2}$的方程(1)的两个实值解。

设我们写成$\boldsymbol{\xi}^{(1)}=\mathbf{a}+i \mathbf{b}$，其中$\mathbf{a}$和$\mathbf{b}$是实数；那么我们有

$$\begin{equation*} \mathbf{x}^{(1)}(t)=(\mathbf{a}+i \mathbf{b}) e^{(\lambda+i \mu) t}=(\mathbf{a}+i \mathbf{b}) e^{\lambda t}(\cos (\mu t)+i \sin (\mu t)) \tag{15} \end{equation*}$$

将$\mathbf{x}^{(1)}(t)$分离成实部和虚部，我们得到

$$\begin{equation*} \mathbf{x}^{(1)}(t)=e^{\lambda t}(\mathbf{a} \cos (\mu t)-\mathbf{b} \sin (\mu t))+i e^{\lambda t}(\mathbf{a} \sin (\mu t)+\mathbf{b} \cos (\mu t)) \tag{16} \end{equation*}$$

如果我们写成$\mathbf{x}^{(1)}(t)=\mathbf{u}(t)+i \mathbf{v}(t)$，那么向量

$$\begin{align*} & \mathbf{u}(t)=e^{\lambda t}(\mathbf{a} \cos (\mu t)-\mathbf{b} \sin (\mu t)) \\ & \mathbf{v}(t)=e^{\lambda t}(\mathbf{a} \sin (\mu t)+\mathbf{b} \cos (\mu t)) \tag{17} \end{align*}$$

是方程(1)的实值解。可以证明$\mathbf{u}$和$\mathbf{v}$是线性独立的解(参见问题22)。

例如，假设矩阵$\mathbf{A}$有两个复特征值$r_{1}=\lambda+i \mu$， $r_{2}=\lambda-i \mu$，并且$r_{3}, \ldots, r_{n}$都是实数且互异。令对应的特征向量为$\boldsymbol{\xi}^{(1)}=\mathbf{a}+i \mathbf{b}, \boldsymbol{\xi}^{(2)}=\mathbf{a}-i \mathbf{b}, \boldsymbol{\xi}^{(3)}, \ldots, \boldsymbol{\xi}^{(n)}$。那么方程(1)的通解为

$$\begin{equation*} \mathbf{x}=c_{1} \mathbf{u}(t)+c_{2} \mathbf{v}(t)+c_{3} \boldsymbol{\xi}^{(3)} e^{r_{3} t}+\cdots+c_{n} \boldsymbol{\xi}^{(n)} e^{r_{n} t} \tag{18} \end{equation*}$$

其中$\mathbf{u}(t)$和$\mathbf{v}(t)$由方程(17)给出。我们强调，这种分析仅在方程(1)中的系数矩阵$\mathbf{A}$是实数时才适用，因为只有那时复值特征值和特征向量才必须成共轭对出现。

对于具有实值系数的$2 \times 2$系统，我们现在完成了对可能发生的三种主要情况的描述。这三种主要情况是：

1. 特征值是实数且符号相反；$\mathbf{x}=\mathbf{0}$是鞍点。
2. 特征值是实数且符号相同但不相等；$\mathbf{x}=\mathbf{0}$是节点。
3. 特征值是具有非零实部的复数；$\mathbf{x}=\mathbf{0}$是螺旋点。

其他可能性出现在刚刚列出的两种情况之间的过渡，并且在实际应用中不太可能遇到。例如，零特征值出现在鞍点和节点之间的过渡期间。纯虚特征值出现在渐近稳定和不稳定螺旋点之间的过渡期间。最后，实数且相等的特征值出现在节点和螺旋点之间的过渡期间。

例子 2

系统

$$\mathbf{x}^{\prime}=\left(\begin{array}{cc} \alpha & 2 \tag{19}\\ -2 & 0 \end{array}\right) \mathbf{x}$$

包含一个参数$\alpha$。描述解在质量上如何依赖于$\alpha$；特别地，找到$\alpha$的分岔值，即相平面中轨迹的定性行为发生显著变化的值。

解：

轨迹的行为由系数矩阵的特征值控制。特征方程是

$$\begin{equation*} r^{2}-\alpha r+4=0 \tag{20} \end{equation*}$$

所以特征值是

$$\begin{equation*} r=\frac{\alpha \pm \sqrt{\alpha^{2}-16}}{2} . \tag{21} \end{equation*}$$

从方程(21)可以看出，对于$-4<\alpha<4$，特征值是复共轭，否则是实数。

两个分岔值是$\alpha=-4$和$\alpha=4$，其中特征值从实数值变为复数值，反之亦然。对于$\alpha<-4$，两个特征值都是负的，所以所有轨迹都接近原点，这是一个渐近稳定的节点。对于$\alpha>4$，两个特征值都是正的，所以原点又是一个节点，这次是不稳定的；所有轨迹（除了$\mathbf{x}=\mathbf{0}$）都变得无界。在中间范围$-4<\alpha<4$中，特征值是复数，轨迹是螺旋线。然而，对于$-4<\alpha<0$，特征值的实部为负，螺旋线向内定向，原点是渐近稳定的，而对于$0<\alpha<4$，特征值的实部为正，原点是不稳定的。

第三个分岔值是 $\alpha=0$，此时螺旋线的方向从向内变为向外。当 $\alpha=0$ 时，原点是一个中心，轨迹是围绕原点的闭合曲线，对应于随时间周期性变化的解。另外的分岔值 $\alpha= \pm 4$ 产生实且相等的特征值。在这种情况下，原点又是一个结点，但相图与第 7.5 节中的相图略有不同。我们将在第 7.8 节中讨论这种情况。

多重弹簧-质量系统。考虑图 7.1.1 所示的由两个质量块和三个弹簧组成的系统，其运动方程由第 7.1 节中的方程 (1) 给出。

如果我们假设没有外力，那么 $F_{1}(t)=0, F_{2}(t)=0$，得到如下方程：

$$\begin{align*} & m_{1} \frac{d^{2} x_{1}}{d t^{2}}=-\left(k_{1}+k_{2}\right) x_{1}+k_{2} x_{2} \\ & m_{2} \frac{d^{2} x_{2}}{d t^{2}}=k_{2} x_{1}-\left(k_{2}+k_{3}\right) x_{2} \tag{22} \end{align*}$$

这些方程可以作为一个二阶方程组来求解（参见问题 24），但是，正如我们在本章中所采用的方法一致，我们将它们转化为一个四阶一阶方程组。令 $y_{1}=x_{1}, y_{2}=x_{2}, y_{3}=x_{1}^{\prime}$, 和 $y_{4}=x_{2}^{\prime}$。那么

$$\begin{equation*} y_{1}^{\prime}=y_{3}, \quad y_{2}^{\prime}=y_{4}, \tag{23} \end{equation*}$$

并且，根据方程 (22)，

$$\begin{equation*} m_{1} y_{3}^{\prime}=-\left(k_{1}+k_{2}\right) y_{1}+k_{2} y_{2}, \quad m_{2} y_{4}^{\prime}=k_{2} y_{1}-\left(k_{2}+k_{3}\right) y_{2} \tag{24} \end{equation*}$$

下面的例子处理了一个具有两个质量块和三个弹簧的系统的特殊情况。

示例 3

假设在方程 (23) 和 (24) 中，$m_{1}=2, m_{2}=9 / 4, k_{1}=1, k_{2}=3$, 和 $k_{3}=15 / 4$，那么这些方程变为

$$\begin{equation*} y_{1}^{\prime}=y_{3}, \quad y_{2}^{\prime}=y_{4}, \quad y_{3}^{\prime}=-2 y_{1}+\frac{3}{2} y_{2}, \quad y_{4}^{\prime}=\frac{4}{3} y_{1}-3 y_{2} . \tag{25} \end{equation*}$$

分析由方程 (25) 描述的可能运动，并绘制图形来显示典型的行为。

解：

令 $\mathbf{y}=\left(y_{1}, y_{2}, y_{3}, y_{4}\right)^{T}$。我们可以将系统 (25) 写成矩阵形式：

$$\mathbf{y}^{\prime}=\left(\begin{array}{cccc} 0 & 0 & 1 & 0 \tag{26}\\ 0 & 0 & 0 & 1 \\ -2 & \frac{3}{2} & 0 & 0 \\ \frac{4}{3} & -3 & 0 & 0 \end{array}\right) \mathbf{y}=\mathbf{A y}$$

请记住，$y_{1}$ 和 $y_{2}$ 是两个质量块相对于其平衡位置的位置，并且 $y_{3}$ 和 $y_{4}$ 是它们的速度。我们像往常一样假设 $\mathbf{y}=\xi e^{r t}$，其中 $r$ 必须是矩阵 $\mathbf{A}$ 的特征值，$\boldsymbol{\xi}$ 是对应的特征向量。手工找到 $\mathbf{A}$ 的特征值和特征向量是可能的，虽然有点乏味，但使用适当的计算资源很容易做到。$\mathbf{A}$ 的特征多项式是

$$\begin{equation*} r^{4}+5 r^{2}+4=\left(r^{2}+1\right)\left(r^{2}+4\right) \tag{27} \end{equation*}$$

因此特征值是 $r_{1}=i, r_{2}=-i, r_{3}=2 i$, 和 $r_{4}=-2 i$。对应的特征向量是

$$\boldsymbol{\xi}^{(1)}=\left(\begin{array}{r} 3 \tag{28}\\ 2 \\ 3 i \\ 2 i \end{array}\right), \quad \boldsymbol{\xi}^{(2)}=\left(\begin{array}{r} 3 \\ 2 \\ -3 i \\ -2 i \end{array}\right), \quad \boldsymbol{\xi}^{(3)}=\left(\begin{array}{r} 3 \\ -4 \\ 6 i \\ -8 i \end{array}\right), \quad \boldsymbol{\xi}^{(4)}=\left(\begin{array}{r} 3 \\ -4 \\ -6 i \\ 8 i \end{array}\right)$$

复值解 $\boldsymbol{\xi}^{(1)} e^{i t}$ 和 $\boldsymbol{\xi}^{(2)} e^{-i t}$ 是复共轭，因此可以通过找到其中一个的实部和虚部来确定两个实值解。例如，

$$\begin{align*} \boldsymbol{\xi}^{(1)} e^{i t} & =\left(\begin{array}{r} 3 \\ 2 \\ 3 i \\ 2 i \end{array}\right)(\cos t+i \sin t) \\ & =\left(\begin{array}{c} 3 \cos t \\ 2 \cos t \\ -3 \sin t \\ -2 \sin t \end{array}\right)+i\left(\begin{array}{c} 3 \sin t \\ 2 \sin t \\ 3 \cos t \\ 2 \cos t \end{array}\right)=\mathbf{u}^{(1)}(t)+i \mathbf{v}^{(1)}(t) . \tag{29} \end{align*}$$

以类似的方式，我们得到

$$\begin{align*} \boldsymbol{\xi}^{(3)} e^{2 i t} & =\left(\begin{array}{r} 3 \\ -4 \\ 6 i \\ -8 i \end{array}\right)(\cos (2 t)+i \sin (2 t)) \\ & =\left(\begin{array}{r} 3 \cos (2 t) \\ -4 \cos (2 t) \\ -6 \sin (2 t) \\ 8 \sin (2 t) \end{array}\right)+i\left(\begin{array}{r} 3 \sin (2 t) \\ -4 \sin (2 t) \\ 6 \cos (2 t) \\ -8 \cos (2 t) \end{array}\right)=\mathbf{u}^{(2)}(t)+i \mathbf{v}^{(2)}(t) \tag{30} \end{align*}$$

我们留给您来验证 $\mathbf{u}^{(1)}, \mathbf{v}^{(1)}, \mathbf{u}^{(2)}$ 和 $\mathbf{v}^{(2)}$ 是线性独立的，因此构成了一组基本解。因此，方程 (26) 的通解是

$$\mathbf{y}=c_{1}\left(\begin{array}{r} 3 \cos t \tag{31}\\ 2 \cos t \\ -3 \sin t \\ -2 \sin t \end{array}\right)+c_{2}\left(\begin{array}{c} 3 \sin t \\ 2 \sin t \\ 3 \cos t \\ 2 \cos t \end{array}\right)+c_{3}\left(\begin{array}{r} 3 \cos (2 t) \\ -4 \cos (2 t) \\ -6 \sin (2 t) \\ 8 \sin (2 t) \end{array}\right)+c_{4}\left(\begin{array}{r} 3 \sin (2 t) \\ -4 \sin (2 t) \\ 6 \cos (2 t) \\ -8 \cos (2 t) \end{array}\right)$$

其中，$c_{1}, c_{2}, c_{3}$和$c_{4}$是任意常数。

该系统的相空间是四维的，并且通过方程 (31) 中 $c_{1}, c_{2}, c_{3}$和$c_{4}$ 的一组特定值获得的每个解，对应于此空间中的一个轨迹。由于方程 (31) 给出的每个解都是周期为$2 \pi$的周期解，因此每个轨迹都是一条闭合曲线。无论轨迹在 $t=0$ 时从何处开始，它都会在 $t=2 \pi, t=4 \pi$ 等时刻返回到该点，并在每个长度为 $2 \pi$ 的时间间隔内重复穿过同一条曲线。我们不尝试在此处显示这些四维轨迹中的任何一个。相反，在下面的图中，我们显示了 $y_{1} y_{3}$ - 或 $y_{2} y_{4}$-平面中某些轨迹的投影，从而分别显示了每个质量的运动。

方程 (31) 右侧的前两项描述了频率为 1 且周期为 $2 \pi$ 的运动。请注意，在这些项中，$y_{2}=\frac{2}{3} y_{1}$ 并且 $y_{4}=\frac{2}{3} y_{3}$。这意味着两个质量一起来回移动，始终朝同一方向移动，但是第二个质量的移动距离仅为第一个质量的三分之二，速度也只有三分之二。如果我们将重点放在解 $\mathbf{u}^{(1)}(t)$ 上，并在同一坐标轴上绘制 $y_{1}$ 相对于 $t$ 和 $y_{2}$ 相对于 $t$，则得到幅度分别为 3 和 2 的余弦图，如图 7.6.3(a) 所示。第一个质量在 $y_{1} y_{3}$-平面中的轨迹位于半径为 3 的圆上，如图 7.6.3(b) 所示，从点 (3,0) 开始顺时针行进，并在 $2 \pi$ 时间内完成一个循环。该图中还显示了第二个质量在 $y_{2} y_{4}$-平面中的轨迹，该轨迹位于半径为 2 的圆上，也从 (2,0) 开始顺时针行进，并在 $2 \pi$ 时间内完成一个循环。原点是各自 $y_{1} y_{3}$ - 和 $y_{2} y_{4}$-平面中的中心。从 $\mathbf{v}^{(1)}$ 或从 $\mathbf{u}^{(1)}$ 和 $\mathbf{v}^{(1)}$ 的线性组合可以获得类似的图（时间上有一个适当的偏移）。

方程 (31) 右侧的其余项描述了频率为 2 且周期为 $\pi$ 的运动。观察到在这种情况下，$y_{2}=-\frac{4}{3} y_{1}$ 并且 $y_{4}=-\frac{4}{3} y_{3}$。这意味着两个质量始终朝相反的方向移动，并且第二个质量的移动距离是第一个质量的四分之三，速度也是四分之三。如果我们仅查看 $\mathbf{u}^{(2)}(t)$ 并在同一坐标轴上绘制 $y_{1}$ 相对于 $t$ 和 $y_{2}$ 相对于 $t$，则得到图 7.6.4(a)。存在 $\pi$ 的相位差，并且 $y_{2}$ 的幅度是 $y_{1}$ 的四分之三，这证实了先前关于质量运动的陈述。

图 7.6.4(b) 显示了两个质量在其各自相平面中的轨迹的叠加。两个图形都是椭圆，内部的椭圆对应于第一个质量，而外部的椭圆对应于第二个质量。内部椭圆上的轨迹从 (3,0) 开始，而外部椭圆上的轨迹从 (-4,0) 开始。两者都顺时针行进，并在 $\pi$ 时间内完成一个循环。原点是各自 $y_{1} y_{3}$ - 和 $y_{2} y_{4}$-平面中的中心。再次，从 $\mathbf{v}^{(2)}$ 或从 $\mathbf{u}^{(2)}$ 和 $\mathbf{v}^{(2)}$ 的线性组合可以获得类似的图。

图 7.6.3 (a) 解 $\mathbf{u}^{(1)}(t)$ 的 $y_{1}$ 相对于 $t$ (蓝色实线) 和 $y_{2}$ 相对于 $t$ (红色虚线) 的图。(b) 解 $\mathbf{u}^{(1)}(t)$ 的 $y_{1} y_{3}$ - 和 $y_{2} y_{4}$-平面中轨迹投影的叠加。

图 7.6.4 (a) 解 $\mathbf{u}^{(2)}(t)$ 的 $y_{1}$ 相对于 $t$ (蓝色实线) 和 $y_{2}$ 相对于 $t$ (红色虚线) 的图。(b) 解 $\mathbf{u}^{(2)}(t)$ 的 $y_{1} y_{3}$ - 和 $y_{2} y_{4}$-平面中轨迹投影的叠加。

前两段中描述的运动类型被称为二质量系统的基本振动模式。每种模式都源于相当特殊的初始条件。例如，要获得频率为 1 的基本模式，方程（31）中的常数 $c_{3}$ 和 $c_{4}$ 都必须为零。这仅在初始条件满足 $3 y_{2}(0)=2 y_{1}(0)$ 和 $3 y_{4}(0)=2 y_{3}(0)$ 时发生。类似地，只有当方程（31）中的常数 $c_{1}$ 和 $c_{2}$ 都为零时，即当初始条件满足 $3 y_{2}(0)=-4 y_{1}(0)$ 和 $3 y_{4}(0)=-4 y_{3}(0)$ 时，才能获得频率为 2 的模式。

对于更一般的初始条件，解是两种基本模式的组合。图 7.6.5(a) 显示了一个典型情况下 $y_{1}$ 相对于 $t$ 的图，图 7.6.5(b) 显示了对应轨迹在 $y_{1} y_{3}$ 平面上的投影。请注意，后一个图可能有点误导，因为它显示了轨迹的自相交。在四维空间中，实际轨迹不可能发生这种情况，因为它会违反一般唯一性定理：不可能从同一个初始点发出两个不同的解。

图 7.6.5 满足初始条件 $\mathbf{y}(0)=(-1,4,1,1)^{T}$ 的系统 (25) 的解。(a) $y_{1}$ 相对于 $t$ 的图。(b) 轨迹在 $y_{1} y_{3}$ 平面上的投影。正如文本中所述，四维空间中的实际轨迹不会自相交。